Manip' de la diffraction laser (Mer. 14/09/11)
Première « séance » expérimentale d'après les vacances ; on peut dire que le bilan est (plutôt) positif ! La taille des fils composant le voilage n'est plus un mystère !
Mais commençons par le commencement.
Préparations préliminaires (pléonasme) :
Durant cette séance, nous avons :
• mis en place le montage (boys, laser, voilage, fils…) et mesurer la distance (D) entre l'endroit d'où part le faisceau laser et l'écran ;


• étalonné (pour vérifier) la taille de fils de taille connue à l'aide d'un palmer, alias le "serre-fil-mesureur" ;

Taille des différents fils (en centième de mm) : 10 ; 21 ; 25 ; 28 ; 30 ; 42 ; 44 ; 48 ; 60.
Manipulation :
Nous sommes ensuite passés à la réalisation de la manipulation.
Nous avons placé les fils précédemment calibrés devant le faisceau laser de telle façon qu'ils fassent diffracter le faisceau, et que l'on obtienne une figure de diffraction horizontale.

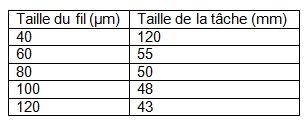
Ensuite, nous avons mesurés la taille des tâches centrales de diffraction, en obtenant ce tableau de valeurs :

Nous nous sommes alors rendus compte que les fils que nous avions choisis étaient trop fins, et avons décidés d'aller au labo des S.V.T. pour faire une estimation de la taille des fils du voilage à l'aide d'un microscope optique.

Micrographie d'une partie du voilage (vue au M.O., x100)

Micrographie d'une « règle » micrométrique (vue au M.O., x100)
Si on superpose les deux micrographies (en positionnant l'extrémité d'un fil au niveau d'un trait) :

Et si on enlève ce qui nous gêne :

Charlie : je m'immisce dans ce magnifique récap pour ajouter ma touche artistique :

L'échelle n'a pas été changée, il s'agit d'une photo X100 comme l'a dit Damien. a+ !
On peut donc constater que la taille des fils composant le voilage est de 0,11 mm environ, soit 110 µm (soit ce que l'on avait trouvé la première fois ! : la formule que l'on avait alors utilisée était en fait fausse, ce qui explique que l'on a jamais pu retrouver le bon résultat).
Connaissant alors l'estimation de la taille des fils, nous avons alors retenté une diffraction du faisceau laser, mais là, avec des fils de 100µm disposés de manière perpendiculaire, comme dans le réseau.



En comparant la figure de diffraction obtenue (notamment, les interférences) avec celle obtenue par le voilage et grâce à l'aide précieuse de Mme Baurrier, nous nous sommes rendus compte qu'il ne faut pas seulement mesurer la taille de la tâche centrale obtenue par la diffraction par le voilage, mais le diamètre du cercle ci-dessous, qui correspond en fait à la taille de la tâche centrale de diffraction d'un seul fil composant le voilage.

A 10,58 m (si mes souvenirs sont bons), on mesure un diamètre de 9,5 cm (contre 11 ou 12 cm pour les fils de 100µm), ce qui confirme la taille de l'ordre de 100µm des fils composant le voilage.
Comme promis, une des captures d'écran du logiciel Mesurim :

Conclusion :
Le mystère de la taille des fils du voilage n'en est donc plus un !
Notre erreur aura été de n'avoir mesuré que le petit rond central de la figure de diffraction par le rideau, ce qui ne nous a pas permis de retrouver, pendant les vacances, la taille des fils qui le composent.
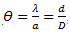 , où :
, où :
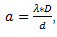 soit a ≈ 0,00125125 m. Soit environ 10 fois plus que ce que l'on pensait.
soit a ≈ 0,00125125 m. Soit environ 10 fois plus que ce que l'on pensait.