Objectif : Cristal tournant
By Charlie Leprince on Thursday 11 August 2011, 17:58 - Expérience du cristal tournant - Permalink
Introduction :
Dans notre tentative pour voir la matière, nous avons, au cours de recherches sur le rayonnement synchrotron, pris connaissance du phénomène de la diffraction des rayons X, qui permet d'analyser un matériau.
Nous allons tenter de reproduire cette expérience à une échelle plus grande que celle de l'atome en utilisant des ondes centimétriques et non des rayons X. La longueur d'onde doit avoir le même ordre de grandeur que la distance interréticulaire, donc pour des cristaux ayant une « distance interréticulaire » de quelques centimètres, il nous faut des ondes centimétriques.
Notre objectif est de réaliser l'expérience du cristal tournant qu'on a pu observer à la faculté de sciences d'Orléans qui permet donc de modéliser ce phénomène de diffraction des rayons X.
Pour cela, nous avons des ondes centimétriques fournies par le lycée, ainsi que le support qui fera varier l'angle entre l'émetteur et le récepteur des ondes mais il nous faut confectionner tout le reste, à savoir les cristaux qui modéliseront la matière et les lentilles.
Les cristaux sont en cours de réalisation et les lentilles on aura le temps d'y revenir, sachant que le professeur de fac qui nous a accueillis, Orélien Randriamboarison, nous a donné ces informations :
Pour la fabrication de la lentille, il vous faut un bloc suffisant de paraffine. Une lentille est constituée par un matériau transparent comprise entre deux surfaces sphériques appelées "dioptres". Un calcul permet d'abord de prévoir les dimensions convenables pour avoir la bonne distance focale. A cela s'ajoute une petite expérience pour connaitre l'indice de réfraction de la paraffine en hyperfréquence. Une fois connue cette valeur n, sur Internet, taper le mot clé : "Maker's formula". Il y a une formule qui vous donne le lien entre distance focale f et les caractéristiques géométriques de la lentille. Le mieux ensuite c'est de trouver à un tourneur-fraiseur à l'atelier du Lycée ou ailleurs, il sera plus à même de vous donner conseil ou directement tailler votre bloc de paraffine.
De toute façon, nous aurons le temps de revenir sur les lentilles à la rentrée.
Donc il est temps de se plonger dans la théorie du cristal tournant. Je vais reprendre mes notes (billet récap'3) et les arranger pour essayer de comprendre le maximum, pour voir à quoi on doit s'attendre et ne pas rester les bras croisés une fois le montage réalisé. Avant la physique expérimentale, la physique théorique (autant que nos possibilités nous le permettent bien sûr).
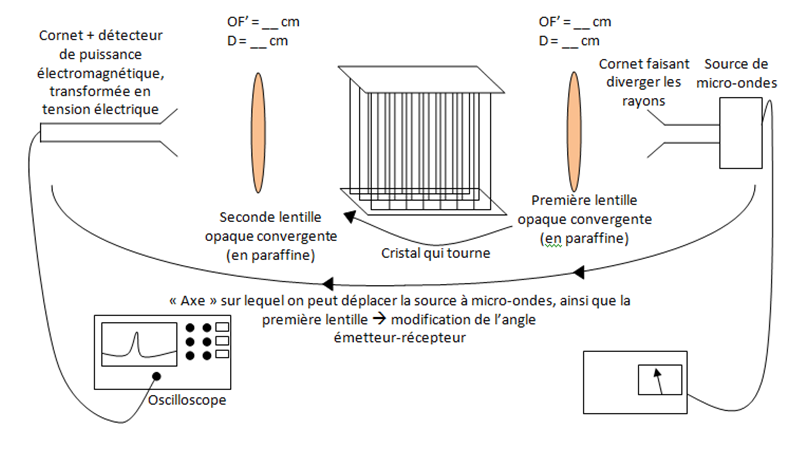
Expérience cristal tournant
Pas besoin de revenir sur les différentes parties du montage, puisque je viens d'en parler (sinon revenir au billet récap'3). Voici juste le schéma de Damien (qui a dû y passer un temps fou) qui est très parlant pour avoir le montage en tête visuellement.
On commence par trouver la longueur d'onde exacte des ondes centimétriques : on ne connait que la fréquence mais c'est amplement suffisant :
Exemple de la fac :
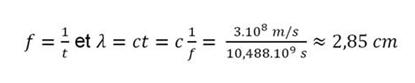
Ce qui va poser quelques problèmes car on rappelle que les ondes du lycée ne comportent que l'indication « environ 10 GHz ». Est-ce que 10.109 s sera assez précis ? On verra.
Avec 10 GHz, la longueur d'onde est de 3 cm…
A partir de là je ne suis pas sûr : mes notes peuvent être complétées par les vôtres, si vous avez des éclaircissements voire tout à redire n'hésitez pas. On pourra de toute façon reposer des questions au professeur de fac ou aux chercheurs du CEMHTI.
Une fois cette longueur d'onde trouvée, on peut trouver théoriquement l'angle pour lesquels une certaine famille du plan diffracte, en utilisant la loi de Bragg.
On doit connaitre la distance d entre les atomes, donc ici entre les tiges du cristal d'une certaine famille : pour la famille 1,0,0 du plan, avec d=4 cm et n=1, on a :
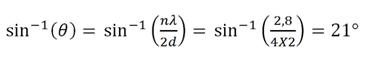
On connait donc l'angle pour lequel la famille diffracte : θ=21x2=42°.
A vérifier expérimentalement.
Expérimentalement
A partir de maintenant je suis dans la supposition (encore plus si c'est possible). Nous passons du côté obscur expérimental.
Supposons que l'on n'ait rien de tout ce que je dis dans la partie théorique (à part peut-être la longueur d'onde). C'est le cas si on se lance dans une expérience pour voir les atomes d'un matériau, ce que l'on veut faire ici.
On fait varier l'angle émetteur/récepteur. Sur l'oscilloscope branché au récepteur (attention, intensité en fonction de l'angle, il faudra faire le lien), on va observer des pics, qui montreront que le cristal a diffracté. Les angles pour lesquels les pics sont les plus grands (car pour 39°, 40° et 41°, si le pic est plus intense à 40° c'est normal car les pics ont une certaine largeur due à la largeur des tiges) sont les angles pour lesquels une famille du plan diffracte.
Pour retrouver cette famille, on utilise encore la loi de Bragg.
Exemple : Si un pic se trouve à 40°, on obtient :
40=20X2 donc θ=20. Ainsi :

Dans ce cas d est donc égal à 4 centimètres environ (sauf erreur de calcul).
On obtient donc la distance interréticulaire de la famille du plan qui diffracte.
On répète l'opération pour les autres angles selon lesquels on retrouve des pics. On obtient donc d'autres distances interréticulaires. Ce qui m'amène à poser une question : comment relier ces différentes distances interréticulaires entre elles pour retrouver la structure du cristal ? En observant les angles selon lesquels les familles diffractent ? En observant la fréquence selon laquelle on retrouve un pic ? Peut-être.
Conclusion
Tout cela me semble plutôt cohérent, qu'en pensez-vous ?
D'autres questions me viennent :
- On a dit que c'est une expérience 2D. Mais dans ce cas pourquoi, lorsqu'on ajoute des billes de métal dans les tiges de verre, on observe des interférences à la base des pics ? (voir avec la fonction sinus cardinal au carré)…
- On va tordre une des tiges de fer dans le cristal pour pouvoir analyser les défauts dans le cristal. Comment pourra-t-on retrouver où le cristal est imparfait ? Que cela va-t-il changer ? Peut-être des interférences, car si on a des nouvelles distances interréticulaires ça ne va pas aller. Faudra-t-il comparer cristal parfait/cristal imparfait ? (Si tant est que le cristal réalisé soit parfait, ce qu'on verra dans quelques jours. Y aura-t-il assez de tiges en fer/en verre ??
Voilà, je m'y suis replongé, et malgré quelques questions qui demeurent tout ça me semble plus clair, et nous saurons quoi chercher. Si vous pouvez, vérifiez peut-être les calculs, je n'en suis pas sûr.
On pourra de toute façon poser des questions au prof de fac ou aux chercheurs à la rentrée. J'espère que ça va marcher, mais il n'y a pas de raison.
Comments
"E. T. Whittaker a montré que la fonction sinus cardinal joue un rôle central dans la théorie de l'interpolation sur un réseau de points équidistants1.
Étant donné que la transformée de Fourier de la fonction porte est très couramment utilisée, le sinus cardinal est forcément très présent, notamment en physique ondulatoire (car les phénomènes de diffraction de Fraunhofer sont traités par transformée de Fourier) ainsi qu'en traitement numérique du signal. Plus précisément, en théorie de la communication, la fonction sinus cardinal permet la synthèse exacte des signaux à spectre de support fini (formule de Shannon, 1949). En particulier, le sinus cardinal est fréquemment rencontré en théorie des antennes, en acoustique, en radar, pour la diffraction par une fente, etc."
de wikipédia
Très bon récap' !
1. Je pense qu'il y a une faute à un endroit. Dans la partie théorique pré-expérimentale, on trouve théoriquement que, pour une distance d valant 4 cm, la famille hkl 1,0,0 fait diffracter les rayons avec un angle de 21°.
Donc, dans la partie expérimentale, pour un angle de 20°, on devrait trouver une distance d d'environ 4 cm (avec une marge d'erreur), ce que je retrouve par calcul.... Donc petit problème à cet endroit là.
D'ailleurs, la recherche théorique du début ne doit être qu'un moyen de vérifier les résultats expérimentaux. Je pense que, ce qui serai mieux, c'est de commencer (si possible) par la partie expérimentale afin de théoriser nos résultats.
2. Je pense que je vais faire, d'ici quelques jours, un billet d'approche concernant la fiche de TP de fac pour cette expérience, afin d'essayer de mieux cerner et comprendre à quoi nous pouvons être amenés à faire.
Et puis ça permettra certainement de répondre à la plupart de nos questions, notamment celle-ci :
"comment relier ces différentes distances interréticulaires entre elles pour retrouver la structure du cristal ? En observant les angles selon lesquels les familles diffractent ? En observant la fréquence selon laquelle on retrouve un pic ? "
-> Pour l'instant, je ne peut pas répondre, mais je pense que non pour les deux, étant donné que l'on n'est pas censés connaître la structure du cristal (triangle ?, carré ?, etc. ?) et, comme le cristal tourne, je ne sais pas si on va pouvoir savoir quelle famille fait diffracter les rayons pour un angle donné (pour lequel on a observé un pic).
3. "On va tordre une des tiges de fer dans le cristal pour pouvoir analyser les défauts dans le cristal. Comment pourra-t-on retrouver où le cristal est imparfait ? Que cela va-t-il changer ? Peut-être des interférences, car si on a des nouvelles distances interréticulaires ça ne va pas aller." --> >Seuls les résultats de la manip' nous le diront.
"Faudra-t-il comparer cristal parfait/cristal imparfait ?" --> Je pense que oui, c'est nécessaire, pour pouvoir voir ce qui change entre le cristal "parfait" et le cristal imparfait.
Retour au 2. Parce qu'expérimentalement, on connait juste l'angle entre l'émetteur et le récepteur. Par la loi de Bragg, on retrouve la distance interréticulaire.
En fonction du nombre de distance "d" que l'on va trouver, on sera peut-être plus à-même de trouver la structure du cristal (je dis bien le nombre de "d") en trouvant pour chaque structure de cristal (triangle, carré, etc.) le nombre de distance "d" que chacun peut contenir. Ensuite, on compare ce nombre avec celui trouvé expérimentalement et peut-être (je sais me^me pas si ce que je dis est envisageable) que l'on trouvera la structure du cristal.
Je ne sais pas du tout, ça reste encore un peu vague dans mon esprit. J'espère que la fiche de TP nous aidera là-dessus !
1'. Tu dois avoir raison, il y a sûrement une faute à cet endroit. D'ailleurs si tu pouvais la corriger en changeant l'image du calcul ou un truc comme ça, puisque tu retrouves 4 par le calcul (au pire envoie-la moi je la mettrai).
Cependant c'est bizarre. Pourquoi on devrait retrouver, à un degré près, une distance interréticulaire approchée ? Fonction sinusoïdale donc peut-être qu'un degré ça change pas mal la distance d. Parce que sinon on trouverait toujours les mêmes distances d pour un certain angle, je sais pas si c'est le cas... A voir, c'est pas très clair. Peut-être qu'on se trompe et que c'est plus compliqué que ça...
Et évidemment la théorie viendra confirmer l'expérimental puisque si on modélise l'analyse d'un matériau on part du principe que c'est à nous de déduire la théorie !
2'. Pas bête le billet d'approche de la fiche TP, pense à bien résumer (^^).
"comment relier ces différentes distances interréticulaires entre elles pour retrouver la structure du cristal ? En observant les angles selon lesquels les familles diffractent ? En observant la fréquence selon laquelle on retrouve un pic ? " -> Pourquoi pas selon les intensités des pics retrouvés ? Peut-être que grande intensité = grand nombre de tiges qui diffractent = famille comme 1,0,0 plus que 5,1,0. Si tu vois ce que je veux dire.
« comme le cristal tourne, je ne sais pas si on va pouvoir savoir quelle famille fait diffracter les rayons pour un angle donné (pour lequel on a observé un pic). » -> On le saura visuellement mais c’est de la triche (rappelle-toi le coup du crayon cf récap’3), peut-être qu’il y a un moyen.
« En fonction du nombre de distance "d" que l'on va trouver, on sera peut-être plus à-même de trouver la structure du cristal (je dis bien le nombre de "d") en trouvant pour chaque structure de cristal (triangle, carré, etc.) le nombre de distance "d" que chacun peut contenir. » -> Oulah pas sûr puisque à un « d » correspond une famille du plan, et il y en a plein dans tous les cas : 1,1,0 ; 1,0,0 ; 5,1,0, etc etc. Peut-être que je me trompe.
3’. Oui j’avoue.
Bon comme tu vois je suis beaucoup dans le « peut-être ». On peut éventuellement se tromper du tout au tout, n’avoir rien compris, mais je pense quand même pas. Il doit y avoir des trucs qui nous ont échappés. La fiche TP va sûrement aider.
PS : en fait tu as raison pour l'erreur de calcul, mais ma calculette était en radians, d'où le 1,5 cm au lieu de 4,09332616 cm pour être précis :)
J'ai qu'une seule chose à dire pour l'instant :
"Pourquoi pas selon les intensités des pics retrouvés ? Peut-être que grande intensité = grand nombre de tiges qui diffractent = famille comme 1,0,0 plus que 5,1,0. Si tu vois ce que je veux dire."
--> C'est possible, et même judicieux mais, par exemple, pour les familles hkl (1,0,0) et (1,1,0), il y aura le même nombre de pics qui vont diffracter (mais à des angles émetteur/récepteur différents), mais là, les distances entre les pics de chaque famille sont différentes (plus grande pour 1,1,0). Donc pour certaines familles, c'est certainement possible mais pas pour toutes. Encore faudrait-il savoir de quelle famille il s'agit...
Euh, tu parles bien de pics ou de tiges qui diffractent ? ça m'embrouille un peu tout ça. Mais je crois comprendre ce que tu veux dire. De toute façon c'était une idée comme ça... on verra.