Expérience des billes 1
By Charlie Leprince on Sunday 26 June 2011, 11:35 - Expérience des billes - Permalink
Expérience des billes, essai n°1
25/06/11
Essai en 1D, lampe en-dessous, lampe à incandescence.



Résultats :
|
Longueur (mm) |
Résistance (Ω) |
|
0 |
108,2 |
|
1 |
112,4 |
|
2 |
119,7 |
|
3 |
105,4 |
|
4 |
98 |
|
5 |
99,4 |
|
6 |
102,4 |
|
7 |
101,2 |
|
8 |
99,4 |
|
9 |
101,6 |
|
10 |
92 |
|
11 |
89,6 |
|
12 |
88,4 |
|
13 |
89,1 |
|
14 |
89,7 |
|
15 |
87 |
|
16 |
83,7 |
|
17 |
80,5 |
|
18 |
77,3 |
|
19 |
77,7 |
|
20 |
75 |
|
21 |
76 |
|
22 |
76,5 |
|
23 |
76 |
|
24 |
75,8 |
|
25 |
75,1 |
|
26 |
75,5 |
|
27 |
73,5 |
|
28 |
72,4 |
|
29 |
72 |
|
30 |
69,5 |
|
31 |
71,1 |
|
32 |
71 |
|
33 |
71,8 |
|
34 |
72,5 |
|
35 |
71,7 |
|
36 |
71,9 |
|
37 |
73 |
|
38 |
72,9 |
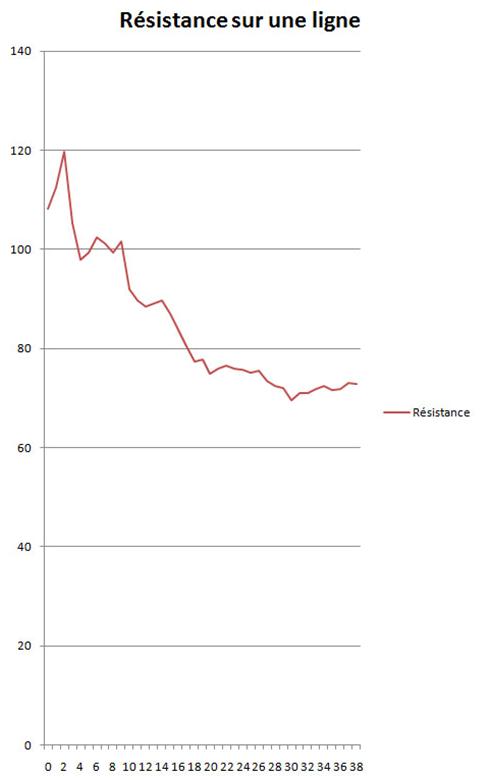
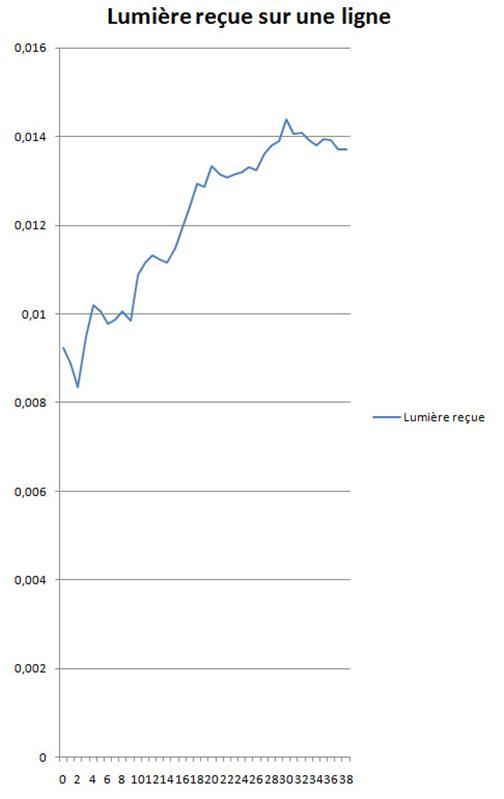
Rappel : plus il y a de lumière plus la résistance diminue car la photorésistance est sensible aux photons : quand il y en a le courant passe mieux.
Donc quand on fait le graphique de la résistance on obtient une courbe inverse de la lumière reçue.
Conclusions :
Résultat très mitigé, comme le montre la courbe.
Formes arrondies parfois reconnaissables, de l'ordre de 4-5 mm. Forte amplitude (50 Ω) et forte baisse de la résistance plus on « avance » sur la ligne, dur probablement au faisceau trop convergent, donc la luminosité est plus importante au niveau d'un point en particulier.
Graphique de la résistance à prendre à l'envers car le principe de la photorésistance indique que plus la résistance est importante plus la luminosité est faible, donc les billes diffusent la lumière lorsque la résistance est plus faible.
A voir : avec une autre lampe
- Moins lumineuse et surchargeant moins la photorésistance (saturation visible dès le faible écart des mesures lorsque la luminosité est plus importante) -> lampe économique ?
- Lampe avec un faisceau plus divergent -> Tube fluorescent ?
Faire des mesures préalables d'un « trou » : mêmes conditions expérimentales mais sans billes, faisceau lumineux traversant le support transparent. Afin de savoir à quel moment on a un trou sur la ligne, afin de vérifier l'homogénéité de la répartition de la luminosité.
Le dispositif s'avère facile à manier, plutôt précis et droit.
Faire des essais avec la lampe au-dessus ?
Schéma :
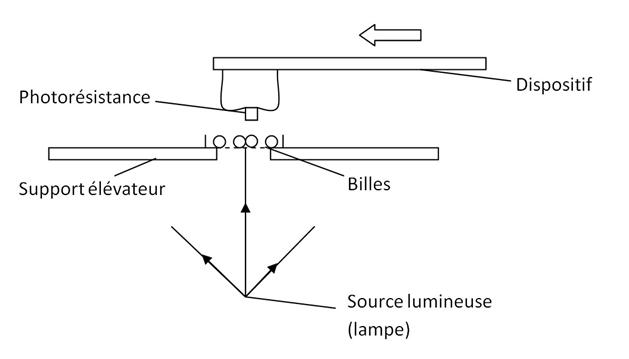
NB : Attention à ne pas faire tomber les billes (oui c'est arrivé).
Comments
Question : Sur ta troisième photo, la lampe éclairant par le bas est allumée ou c'est le flash ? Parce que, s'il s'agit du premier cas, on voit bien qu'il y a un "problème" au niveau de l'éclairage. Ce qui expliquerait, comme tu l'as dit, la forte différence entre les différentes mesures.
Mais je ne pense pas que le faisceau utilisé est trop convergent, étant donné qu'une lampe à incandescence livre une lumière assez diffuse.
De toute façon, c'est la faute du matos ! :D
sympas après on peut essayer de mettre un petit laser que l'on fait viser directement la photo résistance, et on fait bouger les deux en même temps, ce serai peut être plu propre
(genre sur un U d'un côtes un pointeur laser, de l'autre la photorésistance, peut-être infrarouge...)
sa permettra de voir les parassites assimilable à diffraction/difusion, genre moins on a de lumière plus la bille est grosse, ça sort du cadre?
@ Damien : nan la lampe était allumée, comme tu l'as dit on voit bien l'hétérogénéité de la répartition de la luminosité. J'ai fait de mon mieux pour la disposition de la lampe mais bon.
Mais ce n'est pas si étonnant, même avec une lampe à incandescence, rappelle toi son diagramme de diffusion, c'était une "colline" quand même. Si on considère que cette fois la lampe n'est plus à un mètre mais à 10 cm de l'objet éclairé alors les écart si petits ne sont plus vraiment étonnants.
@Yohann : Je vois ce que tu veux dire, même si on n'a pas de laser, on pourra peut-être voir ça si les résultats sont concluants. Et ça sort pas du cadre parce que c'est l'étude de la matière (et donc de ses défauts, de ses caractéristiques) par phénomène d'interaction lumière/matière). A voir, on garde l'idée.