• Récapitulons !

 

Le vendredi 27 mai, nous avons réalisé la diffraction d'un faisceau laser par différents fils de largeurs différentes (40 ; 60 : 80 ; 100 et 120 µm) et noté la taille de la tâche centrale (donc la plus grande) de diffraction. Nous avons obtenu le tableau suivant :

 

 

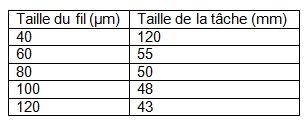
Nous avons ensuite réalisé la diffraction du faisceau laser par le réseau du rideau. On obtient une tâche centrale de diffraction de 4 mm. Nous pensions alors que la taille des fils composant ce réseau était de 110 µm, soit un peu plus d'un dixième de millimètre.

 

Or, dans le livre de Terminale S (référence à trouver), on nous dit que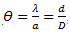, où :

  • λ est la longueur d'onde du faisceau diffracté, ici : λ = 650 nm, soit 650*10-9 m ;
  • a est la largeur du fil (en m) ;
  • d est la moitié de la taille centrale (en m) ;
  • D est la distance qui sépare le fil de l'écran, ici : D = 3,85 m.

 

D'après cette formule, on a : 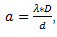soit a ≈ 0,00125125 m. Soit environ 10 fois plus que ce que l'on pensait.

 

Ensuite, en suivant ce qui est dit sur ce site (http://physiquehenner.net/Seconde/Lumiere/Diffractionmathscor.htm) et sur le livre de seconde (Physique Chimie 2nde, Belin), nous avons tracé le graphique représentant la taille de la tâche (L, en m) en fonction de l'inverse de la taille du fil (a-1, en m-1). On obtient alors une droite passant par l'origine du repère, d'équation : L = 4,38*10-6 * a-1. D'où a = 4,38*10-6 * L-1.

 

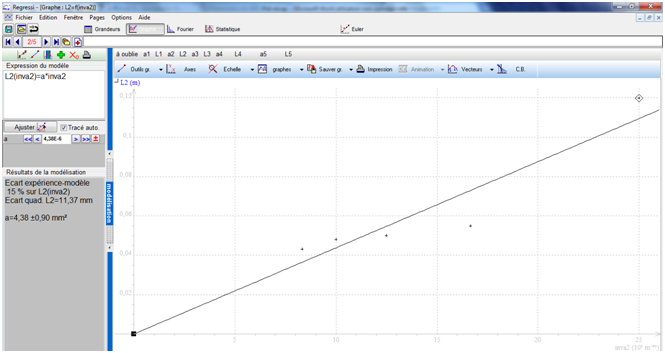
Pour notre réseau, L= 0,004 m, d'où a = 1,095*10-3 m. Ce qui est totalement différent des précédents résultats.

 

 

• Tentons d'avancer !

 

En calculant la longueur d'onde à l'aide de la formule du livre de Terminale S et en comparant le résultat obtenu avec la valeur théorique de λ, on observe que les deuxième et troisième valeurs du tableau sont éloignées de ce qu'elles devraient être. On les enlève (une par une, d'abord la plus éloignée (la deuxième), puis les deux) pour faire un nouveau Regressi, et on obtient la formule L = 4,95*10-6 * a-1. D'où a = 4,95*10-6 * L-1. Le tout avec un écart relatif de 3,6 %. On a certes moins de valeurs, mais un écart relatif inférieur à 5%.

Il y a toujours une divergence au niveau de la taille des fils du réseau (on obtient ici 1,2375*10-3 m).

 

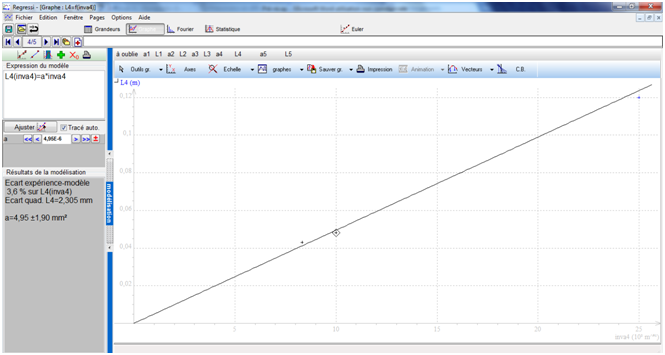
(Les lectures graphiques confirment ces résultats).

 

Attention : Sur le site (je n'ai pas réussi à y aller aujourd'hui), on exprime L (en cm, et non pas en m) en fonction de a-1 (en m-1). Du coup, on obtient avec la dernière formule a = 1,24*10-5, ce qui correspondrait au résultat que l'on attend.

Et si on met L en cm pour faire un graphique avec Regressi, la valeur du coefficient directeur ne change pas (plutôt étonnant, j'aurais pensé que cela aurait rajouter un 10-2 à ce coefficient).

Mais il faut faire très très attention aux unités (je ne me suis trompé plusieurs fois…) !

 

 

• Pistes de recherches

 

1/ J'ai pensé, comme l'on obtenait des « petits carrés » sur la figure de diffraction, que l'on pourrait prendre l'aire du plus grand carré au lieu de prendre juste la valeur d'un de ses côtés, mais cela m'a amené à penser que notre expérience ne fait pas parti des diffractions par une fente/un fil, mais plutôt comme une diffraction par un réseau de trous carrés. Donc on aurait plus affaire à une expérience de seconde. Et on pourrait être amené à réaliser quelque chose comme ceci :

Issu de http://lagouge.ecole-alsacienne.org/10-11/cahier_texte_TS4/TP%20physique/Diffraction.pdf

 

En connaissant i, on pourrait calculer a, puis n. Ainsi, on connaitrait le nombre de fils par millimètre et l'espacement entre ceux-ci, donc on pourrait connaitre leur taille…

A approfondir.

 

2/ C'est tout bête, mais je n'y avais pas pensé.

On a un réseau de fil comme ceci :

 

Chaque fil fait diffracter le faisceau laser, et la figure de diffraction est perpendiculaire au fil. De sorte que sur la figure finale, on obtient l'image des fils comme ceci :

 

(A partir de là, c'est moins bête…)

Or, on obtient cela :

http://melusine.eu.org/syracuse/mluque/fresnel/augustin/images/diffecranRectangle1.jpg

 

On peut donc supposer que la figure de diffraction d'un fil cache la figure de diffraction d'un autre fil (vous me suivez ?) et il faudrait voir s'il n'y a pas un moyen de décomposer la figure finale pour retrouver la figure de diffraction d'un fil afin de connaître la taille de celui-ci.

 

 

• Conclusion :

Il faut réfléchir à tout ça, voir si c'est possible de trouver notre solution à partir de nos mesures ou grâce à d'autres méthodes…