Introduction :

Dans ce billet, nous allons essayer de mieux comprendre ce qui va nous attendre pour la réalisation de la manipulation du cristal tournant. Surtout, il ne faut pas oublier que c'est un billet d'approche ; il n'expliquera pas tout dans les détails, mais essayera d'être le plus précis possible.

Néanmoins, le but principal de cette approche est de répondre à nos interrogations, et notamment celle concernant la mise en relation des différentes distances interréticulaires trouvées afin de reconstituer (sans tricher !) la structure de nos cristaux.

La fiche TP s'organise de la façon suivante :

  1. But de la manipulation
  2. Rappels théoriques (expliqués pour la plupart ci-dessous) concernant les distances réticulaires, la loi de Bragg et la méthode du cristal tournant
  3. Montage expérimental

 

Rappels :

Un cristal, base de la cristallographie, est un solide polyédrique à structure régulière et périodique, formé d'un empilement ordonnée d'atomes, de molécules ou d'ions.

L'étude de ceux-ci (qui ont pour ordre de grandeur l'Angström) se fait généralement à l'aide de la diffraction des rayons X ; expérience régie par la loi de Bragg, définie par la relation nλ= 2d.sin(θ), où n est l'ordre de diffraction (nombre entier supérieur ou égal à 1), λ la longueur d'onde du rayonnement, d la distance interréticulaire et 2θ l'angle entre le faisceau « incident » et le faisceau diffracté.

Il existe trois méthodes d'étude des cristaux à l'aide des rayons X : la méthode de Laue (nécessitant un rayonnement polychromatique), la méthode des poudres (je suppose, celle utilisée au CEMHTI (CNRS)) et celle du cristal tournant, que l'on cherche à modéliser à l'aide d'ondes hyperfréquences.

 

Notions apportées :

Souvent, on définit l'état cristallin comme une juxtaposition de petits parallélépipèdes égaux entre eux (dans notre cas, il s'agira de parallélépipèdes particuliers : des cubes). Les sommets de ces parallélépipèdes sont appelés nœuds.

Une rangée de nœuds passant par une origine O arbitrairement choisie et un nœud u v w est notée [u v w] (où u, v et w sont des coefficients respectivement associés aux vecteurs , et (plus bas) qui permettent de déduire par translation les nœuds à peu essentiel pour l'instant, c'était juste pour expliquer l'origine de ces coefficients). 7

 

Tout plan passant par trois nœuds non colinéaires est un plan réticulaire.

Une famille de plans réticulaires, dont l'orientation s'exprime grâce aux indices de Miller (et pas d'Hemingway) h, k, l, contient l'ensemble des nœuds du réseau.

L'ensemble des plans est désigné par (h k l), tandis que les rangées par [h k l]. Si l'on prend des axes orthogonaux, les rangées sont normales aux plans. 7

 

Enfin, on considère trois vecteurs , et non coplanaires formant un trièdre de référence. Le plus simple serait de prendre un trièdre direct, à savoir avec représentant l'abscisse, représentant l'ordonnée et la côte.

Pour une famille de plans donnée, il me semble (le lien n'est pas très explicite dans la fiche TP) que la distance a (qui serait issue du vecteur éponyme) correspond à la distance entre chaque plan, b la distance entre chaque nœud d'un plan et c, étant donné que l'expérience se fait en deux dimensions, est nul.

 

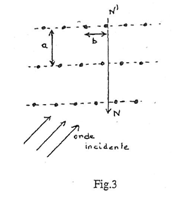Issu de la fiche TP.

 

 

L'expérience du cristal tournant :

 

1/ Dans la « réalité » :

On place dans une chambre cylindrique un monocristal qui tourne autour d'une de ses rangées [u v w], qui coïncide à l'axe de la chambre. On envoie un faisceau étroit de rayons X perpendiculairement sur ce cristal. Quand une famille de plans réticulaires (hkl) correspond à un angle θ et donc quand la loi de Bragg est vérifiée, on observe la diffraction du faisceau de rayons X.

Ces derniers sont « récupérés » sur un film photographique enroulé sur la surface cylindrique de la chambre, sur lequel on peut observer des tâches de diffraction. Elles sont disposées en strates (lignes droites) parallèles et perpendiculaire à l'axe de rotation.

On appelle strate équatoriale celle qui contient le faisceau incident. C'est d'ailleurs sur celle-ci que nous nous serions intéressés (étant donné que notre manipulation se fait en 2D) si nous réalisions cette expérience.

 

Schéma :

 

Par exemple, pour le chrome (pas choisi au hasard), on obtient ceci :

 

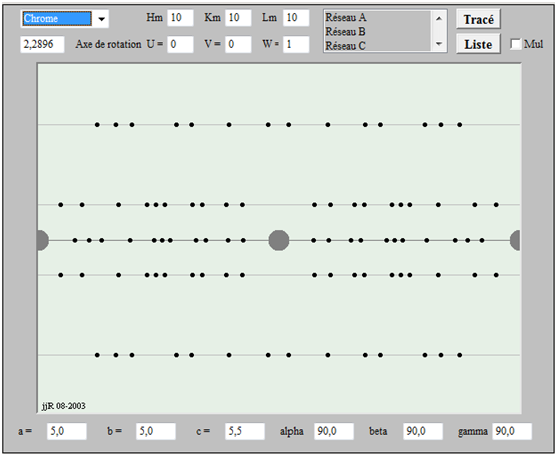
Issu de http://ressources.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/cristallo/cristour.html?width=80%2525&height=80%2525&jqmRefresh=false

 

2/ En TP :

 

• On s'intéresse à la strate équatoriale. En effet, son plan, qui est un plan d'incidence, contient le faisceau incident et les taches de diffraction.

• On se place dans le cas de réseaux trirectangles : tous les angles entre les vecteurs de base sont droits. La strate équatoriale contient les axes d'abscisse et d'ordonnée.

• Etant donné que l'expérience se fait en 2D, on peut omettre l'indice l (qui est nul). Les familles de plans sont désignées par (hk0).

 

Les directions de diffraction :

 

Nous arrivons alors à notre problème principal : comment relier distance interréticulaire afin d'obtenir la structure du cristal.

Il faudrait pour ceci trouver quelles familles de plans font diffracter les rayons X selon un angle donné.

Pour cela, deux pistes :

  • La première, que je ne saisis pas très bien.

 

« En pratique, les réseaux étudiés modélisent des réseaux cubiques : a=b=c. Pour obtenir les angles θ connaissant a (=d) et λ (problème direct), on peut résoudre l'équation de la loi de Bragg (commentaire : ce qui revient à faire θ = Arcsin (nλ/2d)). On obtient ainsi une série d'angles θ<90°, correspondant chacun à un indice (hk) donné. On obtiendra d'autant plus de solutions différentes que le rapport a/λ est grand. Remarquons que l'on obtient la même solution en changeant le signe des indices, ainsi qu'en échangeant h et k. Considérons maintenant dans le plan de rotation une trace (hk) associée à la solution θ. (Commentaire : on considère, mais comment on la trouve ?!!) Lorsque le cristal tourne, dès que cette droite fait l'angle θ avec Ri (Rayon incident je suppose), il se produit une réflexion de Bragg que l'on peut détecter dans la direction 2θ. Cela se produit au moins quatre fois lors d'une révolution, car l'on retrouve exactement la même configuration tous les quarts de tour. Lorsque h et k sont différents et que les traces (hk) et (kh) font un angle aigu, le détecteur placé à 2θ sera illuminé deux fois dans un quart de tour, soit huit fois au cours d'une révolution complète. Si la direction de diffraction ne correspond pas à une réflexion de Bragg, aucun signal ne sera en principe détecté. » de la fiche TP.

 

 

Ou peut-être que je me trompe. C'est n'est peut-être pas du tout en rapport avec notre problème.

 

 

La manipulation :

 

 

Concernant le montage, pas vraiment besoin de blabla je pense ; ce schéma suffira certainement.

 

 

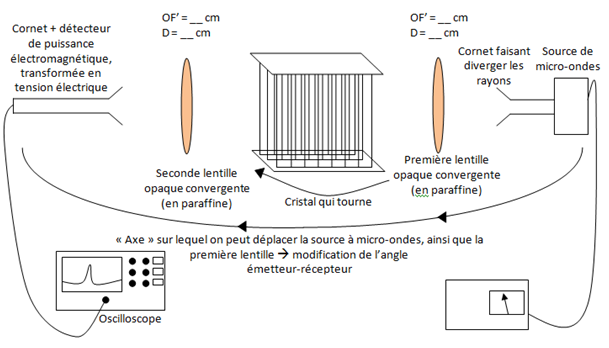
Ou encore :

 

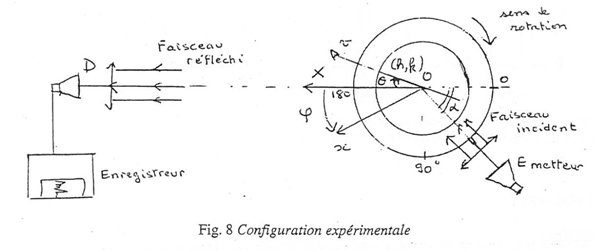
Issu de la fiche TP

((h,k) est le plan qui fait diffracter le rayon)

 

On notera quand-même :

Issu de la fiche TP

 

... et notamment les deux dernières phrases. Peut-être qu'elles sont solutions à nos interrogations. Mais aussi :

 

Concernant le TP en lui-même, et plus particulièrement, la manip' avec le cristal en tiges de fer.

Il faut d'abord : calculer la longueur du signal (donc problème pour nous…), mesurer le(s ?) pas du réseau et faire une résolution théorique, à savoir calculer la série d'angles de Bragg, associés aux indices h et k. Puis indiquer sur un croquis les directions des différents plans permettant une diffraction suivant la loi de Bragg.

Et enfin faire les mesures et interpréter, sans beaucoup plus d'indications, si ce n'est « tracez le graphe de l'intensité des pics (10), (11), (12) et (21) en fonction des directions d'incidence » et « pour identifier les pics, vous pouvez vous baser sur : leur nombre pendant une rotation, les angles d'incidence pour lesquels ils sont observés, mais aussi leur position en azimut ».

 

 

Conclusion :

 

Pas de grandes avancées selon moi, mise à part la prise de connaissance de la fiche TP, des informations qu'elle contient. Cependant, on a d'autres pistes de recherche pour essayer de comprendre comment il est possible de retrouver la structure du cristal, mais sans que ce soit réellement concluant.


Commentaires

Charlie :

J’ai pris des notes aussi, et je vais essayer de résumer des petits trucs qui peuvent être importants, ne serait-ce qu’au niveau du vocabulaire.

 

- 2θ : angle entre faisceau incident et faisceau émergent

 

- On réalise un « modèle analogique à grande échelle ».

 

- Les points du réseau forment un ensemble de centres diffusants.

 

- Tout plan passant par 3 nœuds non colinéaires est un plan réticulaire. Par chaque nœud, on peut faire passer un plan parallèle au plan considéré, donc l’ensemble des nœuds du réseau est compris dans une famille de plans réticulaires, désignés par les plus petits entiers (h k l) tels que les plans considérés coupent les axes du trièdre cristallin à des intervalles égaux à a/h, b/k et c/l. => Alors là j’ai pas tout compris, surtout la désignation de h, k et l, mais… Rappel : a, v et c non coplanaires forment le trièdre de référence : la maille.

 

- Pour obtenir les angles θ connaissant a et λ, on peut résoudre la loi de Bragg et on obtient une série d’angles θ<90° (série finie) correspondant chacun à un ensemble d’indices (h k) donnés.

 

- Lorsque le cristal tourne, dès que la droite de la famille fait l’angle θ avec Ri, il y a « réflexion » de Bragg que l’on peut détecter dans la direction 2θ.

 

- La position des plans réflecteurs est déterminée par la trace des tiges dans le plan horizontal => ???

 

- Dans un réseau cubique,

 

maths12

 

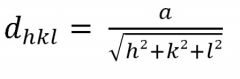
Grâce à ça on retrouve les distances réticulaires des familles.

a : distance entre les plans réticulaires

 

- On connait la distance réticulaire qui correspond à une certaine famille, par théorie.

Pour la partie expérimentale, peut-on partir de rien ? Sans savoir si le cristal est cubique, la distance entre les tiges ? On retrouve la distance d qui correspond à une famille, mais quelle famille ?

Si on connait d et a, on obtient une équation à deux inconnues : h² + k² = (ad)²

 

- a = d ?

a : distance entre les plans réticulaires (plans parallèles au plan réticulaire de « base ») mais pas distance entre les nœuds. Nuance (?)…

Ainsi a = d pour d10 et d01.

Imaginer le cristal, tracer des plans verticaux. Ces plans sont distants de a (vecteur de la maille), mais peuvent couper des nœuds éloignés, comme famille 5,1.

Donc a n’est pas toujours égal à d.

 

Peut-être que je me trompe, c’est pas très clair.

 

- Pour identifier les pics, vous pouvez vous baser sur leur nombre pendant une rotation, les angles d’incidence pour lesquels ils sont observés, leur position en azimut. (La périodicité des pics s’explique grâce à la famille qui diffracte.)

Voilà ce que j'ai noté, ça soulève quelques questions (et oui encore héhé).