Récap’ 12
By Damien TOUSSAINT on Sunday 13 November 2011, 19:33 - Récaps - Permalink
Déjà le douzième récapitulatif de ces ONP… Et le trente-et-unième billet de ce blog…
Ca sent la première finalité qui arrive, c'est-à-dire le concours du 7 décembre (à domicile !), précédé d'un oral blanc le 28 novembre (s'il vous plait, pas de JAPD ce jour-là) qui nous a été très gentiment proposé par les chercheurs du CEMHTI.
Ce récap' s'inscrit dans la continuité du récapitulatif de Charlie, car l'expérience du cristal tournant marche (ou, peut-être devrait-on dire qu'elle tourne rond), le dossier avance et l'on a pu rencontrer le cristallographe afin de mieux comprendre l'exploitation que l'on peut faire des pics de diffraction.
Lundi 07/11/11 :
La première petite manip' que nous avons tenté de réaliser est la détermination expérimentale de la distance focale des lentilles réalisées, via la formule du programme de première :
Voici le montage expérimental :
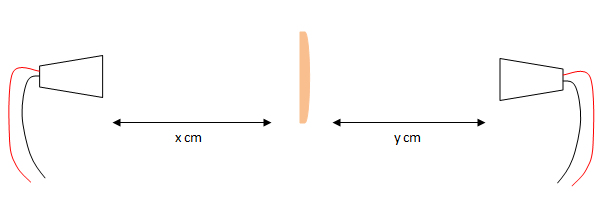
Le but est de trouver à quelles distances x et y on obtient le plus de signal.
En faisant plusieurs mesures (je ne détaillerai pas les calculs), on trouve une focale f' d'environ 35 cm.
C'est ce même jour que nous avons mis en place le montage quasi-définitif de la manip' du cristal tournant, grâce à l'ingénierie de Yohann.
Espérons que le labo de physique n'utilise ni tige, ni noix en ce moment, car l'inventaire risque d'être plutôt léger, vu que l'on monopolise tout ce petit matériel.


Ce montage, datant de lundi, a été amélioré mercredi.
Toujours avec le même protocole expérimental, nous avons réalisé quelques mesures en faisant varier l'angle émetteur-récepteur, et en observant, notamment pour le cristal en tiges de fer, le retour d'un signal, signe de diffraction, pour des angles de 44°, 64° et 90° environ.
Même observation pour le cristal de verre, avec des angles un peu différents, mais diffraction quand même. Preuve que l'on a réalisé de beaux cristaux !
On a même pu récupérer les résultats grâce à la sortie USB d'un oscilloscope numérique de prépa.
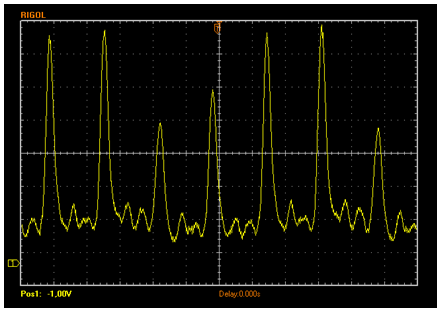
Mercredi 09/11/11 :
Ou comment mêler théorie et pratique…
C'est le jour de la venue du cristallographe au lycée.
Après la mise en place de tout le montage (il faut préciser que le montage, nécessitant 9m² d'espace, donc à peu près huit tables de cours, n'est pas fixe et qu'il demande donc un certain temps pour être assemblé), et la prise de quelques mesures, nous accueillons le cristallographe.
Suite à la présentation de l'expérience, nos regards se tournent sur le cristal de verre, qui semble s'être stabilisé dans sa dégradation (peut-être n'avons-nous pas assez extrudé !), et dans lequel aucun ordre ne semble apparaître… Ce n'est pas un réseau cubique, ni cubique face centrée, mais plutôt triclinique (sans l'être totalement). Dans un réseau triclinique, un atome (ici, une bille) est censé avoir six proches voisins formant un hexagone, ce qui n'est pas vraiment le cas dans notre cristal.

On observe quand même de la diffraction avec ce cristal qui n'est que peu symétrique.
Il faut noter que le réseau triclinique est un des sept systèmes cristallins (cubique, tétragonal, hexagonal, trigonal, orthorhombique, monoclinique et triclinique), caractérisé par a≠b≠c (les vecteurs caractérisant le système cristallin ne sont pas coplanaires), donc par trois angles différents, mais qui permet la diffraction grâce à la juxtaposition de maille, formant un système cristallin.
Cependant, dans notre cristal (pas tout à fait triclinique), il y a très peu de mailles ; c'est une des raisons pour lesquelles on observe une diffraction (la loi de Bragg s'appliquant de préférence à des systèmes infinis).
On dit de quelque chose qu'il est « cristallisé » quand les atomes dont disposés périodiquement dans les plans non coplanaires.
On peut décrire décrire une structure à partir de plans atomiques : l'ensemble des plans parallèles à un autre contient tous les atomes de la structure et donc un système cristallin peut se décomposer en différents plans.
Sur l'oscilloscope, on peut noter la présence de pics. A chaque pic correspond un plan qui diffracte. L'intensité de ces pics est due à la densité des familles de plans considérées ; leur épaisseur, au facteur de Lorentz.
Un pic correspond à la vérification des conditions de Bragg, c'est-à-dire : nλ = 2dhkl.sinθ.
A une famille de plans donnée correspond donc un seul angle de diffraction.
S'il n'y a pas diffraction, alors l'intensité reçue est nulle et on est dans le cas d'interactions destructives. Inversement, si l'intensité est bien renvoyée, alors on est dans le cas d'interférence constructive.
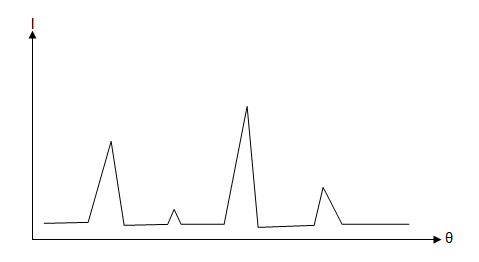
Avec un diffractogramme (faire le lien avec l'oscilloscope), il est possible de retrouver l'angle θ, donc de retrouver d, puis hkl.
Pour tout système cristallin, il existe une relation entre d et hkl.
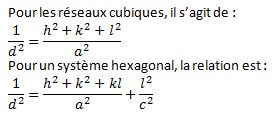
Pour notre cristal en tiges de métal (réseau cubique), a=4.
On peut aussi, pour connaître l'angle pour lequel il va y avoir diffraction, considérer une famille de plan et exprimer d en fonction de a, puis retrouver l'angle θ.
Par exemple, si on considère le plan (1,1,0).
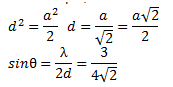
D'où θ=32°, donc on devrait observer un pic pour un angle de 64° (2θ), ce qui est le cas !!
Notons quand même que l'expérience du cristal tournant n'est à l'origine pas destinée à déterminer les familles de plans qui diffractent, mais plutôt à analyser le structure, en déterminant a, b et c.
Il est maintenant possible d'interpréter les pics que l'on observe sur l'oscilloscope. Il y a aussi la méthode des stylos, nous permettant de savoir, en fonction de l'angle de rotation du cristal, quelle famille de plan fait diffracter les faisceaux.
Avancées du week-end :
Déjà la 2.08ième version du dossier…
Le dossier avance, la partie concernant le cristal tournant se remplie bien.
Le poster se complète aussi au fur et à mesure, et le diapo, étant déjà pas mal commencé, avance.
Comments
A noter le caractère aléatoire de la réussite de l'expérience du cristal tournant : on observe parfois de beaux pics pour 44° mais rien pour 64°.
Puis vide intégral jusqu'à 90° environ (c'est le second ordre de 44), et rien à 115°. Bizarre qu'on capte le second ordre mais rien pour la famille 1,1,0, pourtant on a tout remesuré réaligné... Des fois on a tout ce qu'il faut, des fois non.
A noter aussi le net progrès dans la rédaction du dossier et dans l travail préparatoire à l'oral.
Futur billet récap'.
A noter aussi que l'oral ne s'est pas trop trop mal passé. Il y a néanmoins des choses à revoir (notamment l'enchaînement des idées, bien expliciter le but, le fil conducteur... et surtout ne pas aller trop vite, tout expliquer). Mais les remarques des chercheurs étaient très constructives : nous les remercions encore !
Bon alors oui, les points sur lesquels axer le travail préparatoire à l'oral.
- Le sommaire, il faut bien se poser et être clair. Expliquer ce qu'est le TPE.
- Le fil rouge, enchaînement des expérience, le but général, voir la matière.
- Les réalisations fabriquées, lentilles, tous les éléments du montage du cristal tournant, le montage de l'expérience des billes, toute proportion gardée.
- La théorie, bien tout poser, expliquer chaque chose.
- Réduire les diapos.
- L'expérience se fera au sol, éventuellement 2ème vidéoprojecteur avec webcam pour bien voir.
- Travailler la répartition des rôles, et la chorégraphie dans l'espace.
Voilà, on a le temps, en 20 minutes. Enfin pas trop quand même...